II. Application numérique : le bol

0. Importation des librairies

1. Géométrie et maillage du cylindre

# Initialisation du plotteur PyVista en dehors de la fonction
p = pv.Plotter(notebook=True)
p.set_background("grey")


# Fonction pour créer et visualiser la géométrie
def create_ellipse(rho_x, rho_y, h=0.5, lc=0.01):
    global domain
    gmsh.initialize()
    # gmsh.mash.getInfo()

    gmsh.option.setNumber("General.Terminal", 1)
    gmsh.model.add("ellipse")

    # Création de l'ellipse
    ellipse = gmsh.model.occ.addEllipse(0, 0, 0, rho_x, rho_y)
    curve_loop = gmsh.model.occ.addCurveLoop([ellipse])
    surface = gmsh.model.occ.addPlaneSurface([curve_loop])

    # Extrusion pour obtenir un cylindre elliptique
    gmsh.model.occ.extrude([(2, surface)], 0, 0, h)
    gmsh.model.occ.synchronize()

    # Configuration du maillage
    gmsh.option.setNumber("Mesh.CharacteristicLengthMin", lc)
    gmsh.option.setNumber("Mesh.CharacteristicLengthMax", lc)
    gmsh.model.mesh.generate(3)

    # Sauvegarde et conversion du maillage
    gmsh.write("ellipse.msh")
    msh = meshio.read("ellipse.msh")
    meshio.write(
        "ellipse.xdmf",
        meshio.Mesh(
            points=msh.points, cells={"tetra": msh.cells_dict.get("tetra", [])}
        ),
    )
    gmsh.finalize()

    # Lecture du maillage avec FEniCSx
    with XDMFFile(MPI.COMM_WORLD, "ellipse.xdmf", "r") as xdmf_file:
        domain = xdmf_file.read_mesh(name="Grid")
        domain.topology.create_connectivity(
            domain.topology.dim - 1, domain.topology.dim
        )

    # Conversion du maillage pour la visualisation avec PyVista
    u_topology, u_cell_types, u_geometry = plot.vtk_mesh(domain)
    u_grid = pv.UnstructuredGrid(u_topology, u_cell_types, u_geometry)

    # Effacer la scène précédente et ajouter le nouveau maillage
    p.clear()
    # Ajout du maillage à la scène de visualisation
    p.add_mesh(
        u_grid,
        show_edges=True,  # Affiche les arêtes du maillage
        scalar_bar_args={
            "title": "u",  # Titre de la barre de couleur
            "title_font_size": 24,
            "label_font_size": 22,
            "shadow": True,
            "italic": True,
            "font_family": "arial",
            "vertical": False,  # Orientation horizontale de la barre de couleur
        },
    )

    # Ajout d'un titre à la visualisation
    p.add_text(r"Cylindre", font_size=24, color="white", position="upper_edge")

    # Ajout des limites de la boîte englobante
    p.show_bounds(color="white")

    # Ajout des axes de coordonnées
    p.add_axes(color="white")

    # Définition de la couleur de fond
    p.set_background("black")

    # Mise à jour de la scène
    p.show()
    # Affichage de la visualisation
    zoom_factor = 0.75  # Réduire la distance de 20%
    
    # Récupérer les coordonnées actuelles
    cam_pos = (1, 1, 1)  # Position actuelle de la caméra
    target = (0, 0, 0.3)  # Point ciblé
    
    # Calcul de la nouvelle position
    new_cam_pos = (
        target[0] + zoom_factor * (cam_pos[0] - target[0]),
        target[1] + zoom_factor * (cam_pos[1] - target[1]),
        target[2] + zoom_factor * (cam_pos[2] - target[2])
    )
    
    # Appliquer la nouvelle position
    p.camera_position = [new_cam_pos, target, (0, 0, 0.5)]

    #p.show()

    return rho_x, rho_y, h, lc


# Widgets interactifs pour a, b, et h
rho_x_slider = widgets.FloatSlider(
    value=0.1, min=0.01, max=0.2, step=0.01, description="Demi-grand axe"
)
rho_y_slider = widgets.FloatSlider(
    value=0.1, min=0.01, max=0.2, step=0.01, description="Demi-petit axe"
)
h_slider = widgets.FloatSlider(
    value=0.5, min=0.1, max=1.0, step=0.1, description="Hauteur"
)
lc_slider = widgets.FloatSlider(
    value=0.015, min=0.01, max=0.1, step=0.01, description="finesse"
)

# Interface utilisateur et fonction interactive
ui = widgets.VBox([rho_x_slider, rho_y_slider, h_slider, lc_slider])
out = widgets.interactive_output(
    create_ellipse,
    {
        "rho_x": rho_x_slider,
        "rho_y": rho_y_slider,
        "h": h_slider,
        "lc": lc_slider,
    },
)

display(ui, out)


# Fonction pour récupérer les valeurs actuelles des curseurs
def get_slider_values():
    current_rho_x = rho_x_slider.value
    current_rho_y = rho_y_slider.value
    current_h = h_slider.value
    current_lc = lc_slider.value
    return current_rho_x, current_rho_y, current_h, current_lc


# Exemple d'utilisation : récupération des valeurs
rho_x, rho_y, h, lc = get_slider_values()
rho = np.array([rho_x, rho_y])  # Demi-axes dans les directions x et y

# Utiliser Panel pour créer un rendu interactif
pn.extension("vtk")

# Créer le titre avec LaTeX
latex_title1 = pn.pane.LaTeX(r'Cylindre', styles={'font-size': '18pt'})

# Ajouter le rendu VTK
vtk_pane1 = pn.pane.VTK(p.ren_win, width=755, height=400)

# Combiner les éléments
interactive_panel1 = pn.Column(latex_title1, vtk_pane1)

# Utiliser Panel pour créer un rendu interactif
interactive_panel1 = pn.pane.VTK(p.ren_win, width=755, height=400)
glue("img1", interactive_panel1)

2. Définition de l’espace fonctionnel

V = fem.functionspace(domain, ("CG", 1, (domain.geometry.dim,)))
u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)

3. Définition des frontière du domaine

3. Visualisation des frontière du domaine

# Création du maillage PyVista à partir des données FEniCSx
grid = pv.UnstructuredGrid(topology, cell_types, x)


def add_plot(ax, marker, color, title, threshold_min):
    """
    Fonction pour ajouter des maillages à une sous-fenêtre de visualisation.

    Args:
    ax: Axe de la sous-fenêtre PyVista
    marker: Tableau des marqueurs pour les cellules
    color: Couleur pour les cellules filtrées
    title: Titre de la sous-fenêtre
    threshold_min: Valeur minimale pour le filtrage des cellules
    """
    # Mise à jour des données de cellule du maillage avec les marqueurs
    grid.cell_data["Marker"] = marker
    grid.set_active_scalars("Marker")

    # Ajout du maillage complet avec les marqueurs
    ax.add_mesh(
        grid,
        show_edges=True,
        color="cyan",
        scalar_bar_args={
            "title": "Boundary Marker",
            "title_font_size": 24,
            "label_font_size": 22,
            "shadow": True,
            "italic": True,
            "font_family": "arial",
            "vertical": False,
        },
    )

    # Application d'un filtre basé sur le seuil pour isoler certaines cellules
    grid_filter = grid.threshold(threshold_min, scalars="Marker")
    ax.add_mesh(grid_filter, color=color, show_edges=True)

    # Ajout du titre et des axes à la sous-fenêtre
    ax.add_text(title, font_size=12, color="white", position="upper_edge")
    ax.add_axes(color="white")


# Configuration de la visualisation PyVista avec 4 sous-fenêtres (2x2)
pl = pv.Plotter(shape=(2, 2))

# Sous-fenêtre 1 : Affichage de toutes les frontières
pl.subplot(0, 0)
add_plot(pl, markers[3], "red", "surface totale", threshold_min=0.5)
zoom_factor = 0.7  # Réduire la distance de 20%

# Récupérer les coordonnées actuelles
cam_pos = (1, 1, 1)  # Position actuelle de la caméra
target = (0, 0, 0.3)  # Point ciblé

# Calcul de la nouvelle position
new_cam_pos = (
    target[0] + zoom_factor * (cam_pos[0] - target[0]),
    target[1] + zoom_factor * (cam_pos[1] - target[1]),
    target[2] + zoom_factor * (cam_pos[2] - target[2])
)

# Appliquer la nouvelle position
pl.camera_position = [new_cam_pos, target, (0, 0, 0.5)]
# Vue isométrique pour subplot 1

# Sous-fenêtre 2 : Affichage de la frontière inférieure
pl.subplot(0, 1)
add_plot(pl, markers[0], "red", "face inférieure", threshold_min=0.5)
zoom_factor = 0.7  # Réduire la distance de 20%

# Récupérer les coordonnées actuelles
cam_pos = (1, 1, 1)  # Position actuelle de la caméra
target = (0, 0, 0.3)  # Point ciblé

# Calcul de la nouvelle position
new_cam_pos = (
    target[0] + zoom_factor * (cam_pos[0] - target[0]),
    target[1] + zoom_factor * (cam_pos[1] - target[1]),
    target[2] + zoom_factor * (cam_pos[2] - target[2])
)

# Appliquer la nouvelle position
pl.camera_position = [new_cam_pos, target, (0, 0, 0.5)]

# Vue isométrique pour subplot 2

# Sous-fenêtre 3 : Affichage de la frontière supérieure
pl.subplot(1, 0)
add_plot(pl, markers[1], "red", "face supérieure", threshold_min=1.5)
zoom_factor = 0.7  # Réduire la distance de 20%

# Récupérer les coordonnées actuelles
cam_pos = (1, 1, 1)  # Position actuelle de la caméra
target = (0, 0, 0.3)  # Point ciblé

# Calcul de la nouvelle position
new_cam_pos = (
    target[0] + zoom_factor * (cam_pos[0] - target[0]),
    target[1] + zoom_factor * (cam_pos[1] - target[1]),
    target[2] + zoom_factor * (cam_pos[2] - target[2])
)

# Appliquer la nouvelle position
pl.camera_position = [new_cam_pos, target, (0, 0, 0.5)]
# Vue isométrique pour subplot 3

# Sous-fenêtre 4 : Affichage de la frontière latérale
pl.subplot(1, 1)
add_plot(pl, markers[2], "red", "surface latérale", threshold_min=2.5)
zoom_factor = 0.7  # Réduire la distance de 20%

# Récupérer les coordonnées actuelles
cam_pos = (1, 1, 1)  # Position actuelle de la caméra
target = (0, 0, 0.3)  # Point ciblé

# Calcul de la nouvelle position
new_cam_pos = (
    target[0] + zoom_factor * (cam_pos[0] - target[0]),
    target[1] + zoom_factor * (cam_pos[1] - target[1]),
    target[2] + zoom_factor * (cam_pos[2] - target[2])
)

# Appliquer la nouvelle position
pl.camera_position = [new_cam_pos, target, (0, 0, 0.5)]

# Vue isométrique pour subplot 4

# Configuration finale et affichage
pl.set_background("black")

#pl.show()

# Utiliser Panel pour créer un rendu interactif
interactive_panel = pn.pane.VTK(pl.ren_win, width=755, height=400)
glue("img2", interactive_panel)

4. Conditions aux limites

# Définition des conditions aux limites de Dirichlet (déplacement nul)
u_D = np.array([0, 0, 0], dtype=default_scalar_type)

# Application des conditions aux limites sur chaque face
bc0_S0 = fem.dirichletbc(
    u_D, fem.locate_dofs_topological(V, fdim, Sigma_0), V
)  # Face inférieure
bc0_Sh = fem.dirichletbc(
    u_D, fem.locate_dofs_topological(V, fdim, Sigma_h), V
)  # Face supérieure
bc0_Sl = fem.dirichletbc(
    u_D, fem.locate_dofs_topological(V, fdim, Sigma_l), V
)  # Surface latérale

5. Propriétés matériau

# Exemple d'utilisation
E = 210e9  # 210 GPa en Pascals
nu = 0.3  # Coefficient de Poisson
mu, lambda_ = calculate_lame_constants(E, nu)

# mu=
# lambda_=

# Widgets pour les constantes élastiques en GPa
mu_input = widgets.FloatText(value=mu, description="μ = ", step=1)
mu_label = widgets.Label(value="Pa")

lambda_input = widgets.FloatText(value=lambda_, description="λ = ", step=1)
lambda_label = widgets.Label(value="Pa")

# Organisation avec les labels d'unité
mu_box = HBox([mu_input, mu_label])
lambda_box = HBox([lambda_input, lambda_label])


# Fonction pour obtenir les constantes élastiques en Pa
def display_elastic_constants(change):
    mu = mu_input.value  # Conversion en Pa
    lambda_ = lambda_input.value  # Conversion en Pa

    # Afficher les valeurs en Pa
    clear_output(wait=True)  # Clear previous output

    return mu, lambda_  # Retourner les valeurs en Pa


# Liaison de la fonction d'affichage aux événements de changement de valeur des widgets
mu_input.observe(display_elastic_constants, names="value")
lambda_input.observe(display_elastic_constants, names="value")

# Affichage des widgets
ui_elastic = VBox([mu_box, lambda_box])
display(ui_elastic)

mu, lambda_ = display_elastic_constants("value")
# Formater pour afficher en GPa
print(f"Module de cisaillement (μ) = {mu / 1e9:.2f} GPa")
print(f"Premier paramètre de Lamé (λ) = {lambda_ / 1e9:.2f} GPa")

Module de cisaillement (μ) = 80.77 GPa
Premier paramètre de Lamé (λ) = 121.15 GPa

6. Définition des chargements

def calculate_force_volumique(rho, g):
    """
    Calcule la force volumique f à partir de la masse volumique rho
    et de l'accélération gravitationnelle g.

    """
    return rho * g


# données
rho = 7850  # Masse volumique de l'acier en kg/m^3
g = 9.81  # Accélération gravitationnelle en m/s^2
fv = calculate_force_volumique(rho, g)

# Définition de la force volumique (nulle dans ce cas)
f = fem.Constant(domain, default_scalar_type((0, 0, -fv)))

7. Fonctions d’essai et de test

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)

8. Forme bilinéaire \(a\)

a = ufl.inner(sigma(u), epsilon(v)) * ufl.dx  # Forme bilinéaire

9. Forme linéaire \(L\)

def update_linear_form(change):
    global L
    selected_surface = change["new"]
    # Mise à jour de la forme linéaire
    L = ufl.dot(f, v) * ufl.dx
    # Mise à jour de l'affichage
    with output:
        output.clear_output(wait=True)
        print(f"force gravitationnelle exercée sur {selected_surface}")

# Attacher la fonction de mise à jour au widget
surface_selector.observe(update_linear_form, names="value")

# Afficher le widget et la sortie
display(widgets.VBox([surface_selector, output]))

# Initialiser l'affichage
update_linear_form({"new": surface_selector.value})

10. Résolution par la formule variationnelle

# Fonction pour mettre à jour le problème
def update_problem(change):
    global problem
    selected_bc = change["new"]
    problem = LinearProblem(
        a,
        L,
        bcs=bc_dict[selected_bc],
        petsc_options={"ksp_type": "cg", "pc_type": "jacobi"},
    )

    # Mise à jour de l'affichage
    with output:
        output.clear_output(wait=True)
        print(f"Encastrement appliqué sur {selected_bc}")

# Attacher la fonction de mise à jour au widget
bc_selector.observe(update_problem, names="value")

# Afficher le widget
display(widgets.VBox([bc_selector, output]))

# Initialisation du problème avec la valeur par défaut
update_problem({"new": bc_selector.value})

# Avant la résolution
start_time = time.time()

11. Résolution du problème

uh = problem.solve()

12. Visualisation des déplacements

# Visualisation
p = pv.Plotter()
p.add_mesh(
    u_grid_warped,
    show_edges=False,
    scalars="u_z",
    cmap="plasma",  # Changer la colormap
    scalar_bar_args={
        "title": "$u_z$",
        "title_font_size": 24,
        "label_font_size": 22,
        "shadow": False,
        "italic": True,
        "color": "white",
        "font_family": "arial",
        "vertical": False,
    },
)
#p.add_text(r"Déplacements $u_z$", font_size=12, color="white", position="upper_edge")
p.add_axes(color="white")
p.set_background("black")

zoom_factor = 0.7  # Réduire la distance de 20%
# Récupérer les coordonnées actuelles
cam_pos = (1, 1, 1)  # Position actuelle de la caméra
target = (0, 0, 0.3)  # Point ciblé

# Calcul de la nouvelle position
new_cam_pos = (
    target[0] + zoom_factor * (cam_pos[0] - target[0]),
    target[1] + zoom_factor * (cam_pos[1] - target[1]),
    target[2] + zoom_factor * (cam_pos[2] - target[2])
)
# Appliquer la nouvelle position
p.camera_position = [new_cam_pos, target, (0, 0, 0.5)]

p.show()

# Créer le titre avec LaTeX
latex_title3 = pn.pane.LaTeX(r'Déplacement $u_z$', styles={'font-size': '18pt'})

# Ajouter le rendu VTK
vtk_pane3 = pn.pane.VTK(p.ren_win, width=755, height=400)

# Combiner les éléments
interactive_panel3 = pn.Column(latex_title3, vtk_pane3)

# Utiliser Panel pour créer un rendu interactif
#interactive_panel3 = pn.pane.VTK(p.ren_win, width=755, height=400)
glue("img3", interactive_panel3)

# Détection des nœuds situés à la base supérieure (z ≈ H)
tol = 1e-6  # Tolérance numérique
top_nodes = np.abs(u_geometry[:, 2] - h) < tol  # Filtre les nœuds avec z ≈ H

# Création du sous-maillage contenant uniquement la base supérieure
u_grid_top = u_grid.extract_points(top_nodes)

# Création d'un maillage déformé pour exagérer les déplacements
u_grid_top_warped = u_grid_top.warp_by_vector("u", factor=100e6)

# Visualisation avec PyVista
ps = pv.Plotter()

# Ajout du maillage filtré
ps.add_mesh(
    u_grid_top_warped,
    show_edges=False,
    scalars="u_z",  # Coloration en fonction de la composante uz
    cmap="plasma",  # Changer la colormap
    scalar_bar_args={
        "title": "uZ",
        "title_font_size": 24,
        "label_font_size": 16,
        "shadow": False,
        "italic": True,
        "color": "white",
        "font_family": "arial",
        "vertical": False,
    },
)

# Configuration de la scène
#ps.add_text(r'Surface $\Gamma_1$', font_size=12, color="white", position="upper_edge")
ps.add_axes(color="white")
#p.show_bounds(color="white")
ps.set_background("black")

# Créer le titre avec LaTeX
latex_title4 = pn.pane.LaTeX(r'Surface $\Gamma_1$', styles={'font-size': '18pt'})

vtk_panel4 = pn.pane.VTK(ps.ren_win, width=755, height=400)

# Accéder au renderer VTK via l'objet PyVista
renderer = ps.renderer

# Obtenir la caméra
camera = renderer.camera

# Obtenir le centre de la scène
center = ps.center

# Calculer la distance de la caméra
bounds = ps.bounds
diagonal = np.linalg.norm(np.array(bounds[1::2]) - np.array(bounds[::2]))
distance = diagonal * 1.5

# Définir la position de la caméra pour une vue isométrique
camera_position = [
    center[0] + distance / np.sqrt(3),
    center[1] + distance / np.sqrt(3),
    center[2] + distance / np.sqrt(3)
]

# Appliquer la nouvelle position de la caméra
ps.camera_position = [camera_position, center, [0, 0, 1]]

# Réinitialiser la caméra pour appliquer les changements
#ps.reset_camera()

# Mettre à jour le pane VTK
vtk_panel4.param.trigger('object')

# Combiner les éléments
interactive_panel4 = pn.Column(latex_title4, vtk_panel4)

# Utiliser Panel pour créer un rendu interactif
#interactive_panel = pn.pane.VTK(ps.ren_win, width=755, height=400)
glue("img4", interactive_panel4)

Visualisation des contraintes de von Mises

13. Comparaison Analytique-Numérique

Maillage (nombre d’éléments)	(u_z(O’)) (théorique) [nm]	(u_z(O’)) (EF) [nm]	Erreur relative (%)
128 (Grossier)	-0.458	-4.516876	1.40
785	-0.458	-4.508939	1.57
1406	-0.458	-4.511100	1.53
3102	-0.458	-4.514429	1.45
10017	-0.458	-4.516689	1.40
73586 (fin)	-0.458	-4.518891	1.36

import matplotlib.pyplot as plt

# Créer un style sombre personnalisé
plt.style.use("dark_background")

# Données d'exemple
elements = [785, 1406, 3102, 10017, 73586]
errors = [1.57, 1.53, 1.45, 1.40, 1.36]

# Appliquer le thème sombre
plt.figure(figsize=(8, 6))
plt.plot(elements, errors, marker="o", color="cyan", label="Erreur relative (%)")
plt.xscale("log")
plt.xlabel("Nombre d'éléments (log)")
plt.ylabel("Erreur relative (%)")
plt.title("Convergence EF : Erreur relative vs Raffinement")

plt.legend()
plt.grid(color="grey", linestyle="--", linewidth=0.5)
plt.show()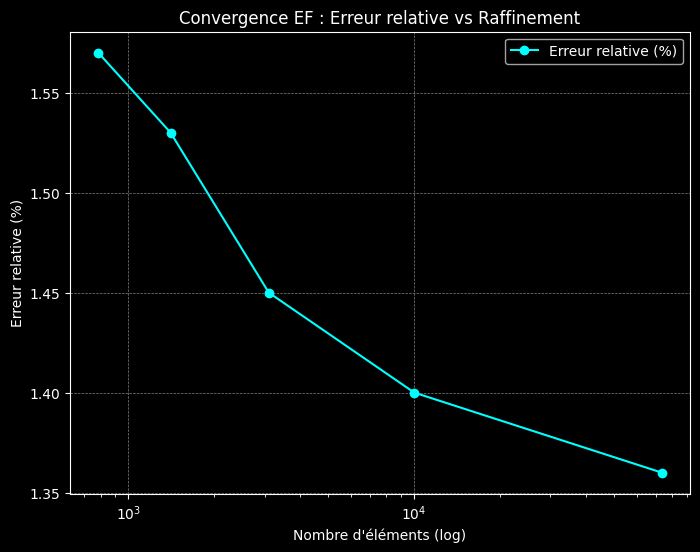

# Utiliser Panel pour créer un rendu interactif
pn.extension("vtk")