1. Résolution de problèmes d’élastostatique linéarisés : l’approche en contrainte
Dans cet exercice, nous étudions le comportement mécanique d’un cylindre soumis à son propre poids. - Dimensions et orientations : Le cylindre a une hauteur \(H\) selon la direction \(\boldsymbol{e}_3\) et un rayon \(R\) pour sa section droite circulaire. - Surfaces principales (voir figure 1.1 ci-dessous): - \(\Gamma_0\) désigne la base inférieure du cylindre située dans le plan \(x_3 = 0\). - \(\Gamma_1\) désigne la base supérieure du cylindre située dans le plan \(x_3 = H\). - \(\Gamma_l\) représente la surface latérale du cylindre. - Point de référence : Le point \(O\) est le centre de la base \(\Gamma_0\).
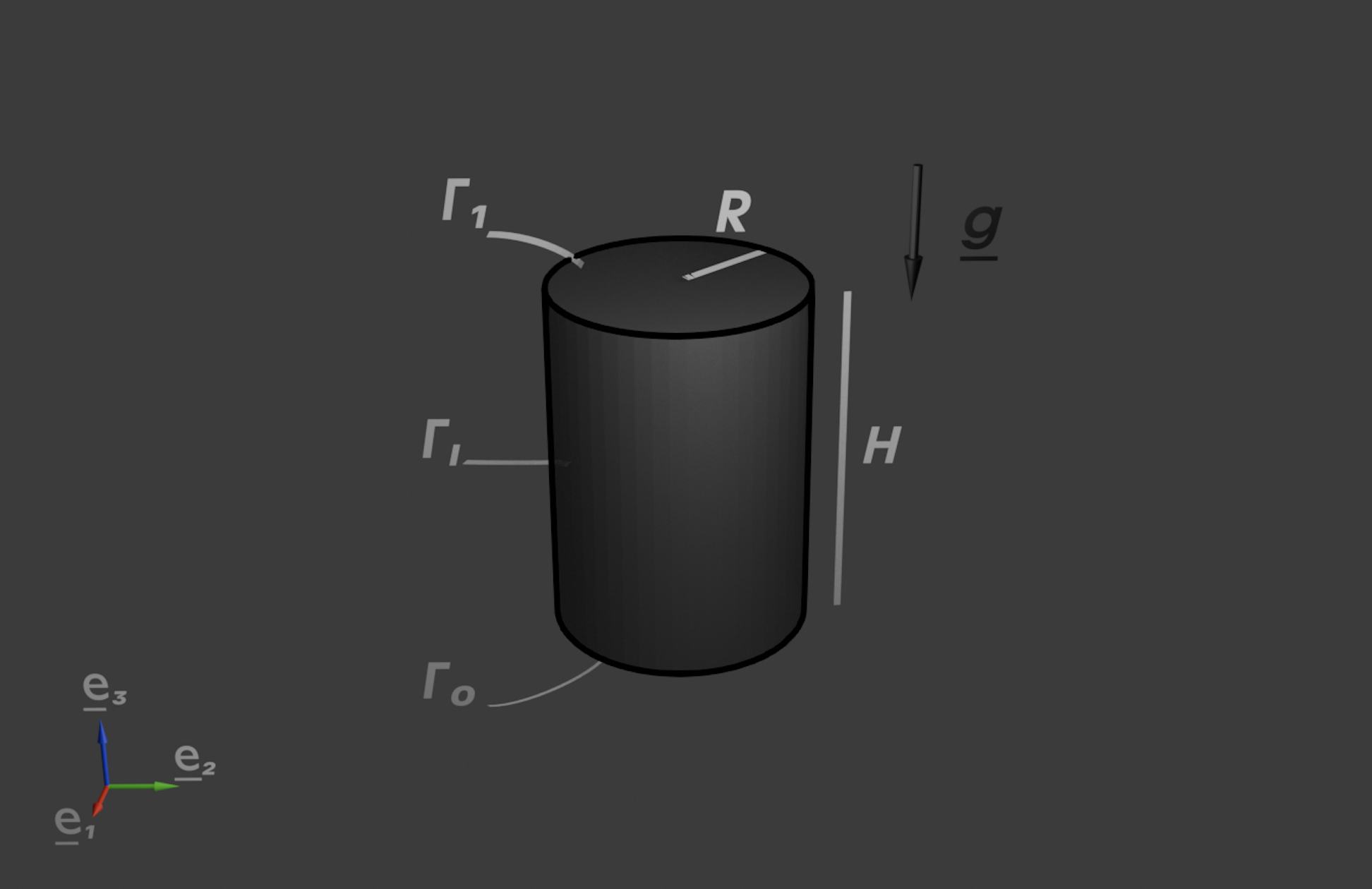 Figure 1.1 : Représentation du cylindre avec ses surfaces principales.
Figure 1.1 : Représentation du cylindre avec ses surfaces principales.
Le cylindre est élastique, homogène et isotrope, caractérisé par un module de Young \(E\) et un coefficient de Poisson \(\nu\). Il est supposé pesant, avec une masse volumique \(\rho\). La base \(\Gamma_0\) est encastrée, tandis que les surfaces \(\Gamma_1\) (base supérieure) et \(\Gamma_l\) (surface latérale) sont supposées libres d’efforts.
- Traduire l’équilibre de la pièce et en déduire la résultante et le moment au point \(O\) du tenseur des efforts surfaciques exercés sur cette base.
Montrer que ce torseur est équivalent à une distribution d’efforts surfaciques uniforme de la forme $_s = P_3 $, où \(P\) étant un scalaire constant que l’on exprimera en fonction des données du problème.
1.1 Établissement des équations d’équilibre
À partir des lois de l’équilibre statique, nous pouvons écrire les relations suivantes :
\[
\begin{cases}
\mathbf{R} + \mathbf{R}^* = \mathbf{0} \\
\mathbf{M}_O + \mathbf{M}_O^* = \mathbf{0}
\end{cases}
\]
où :
- \(\mathbf{R}^*\) désigne la résultante du poids du cylindre,
- \(\mathbf{M}_O^*\) désigne le moment résultant du poids par rapport au point \(O\).
À l’équilibre, la résultante du poids \(\mathbf{R}^*\) est équilibrée par les actions extérieures mécaniques surfaciques appliquées sur la base \(\Gamma_0\). Ces actions s’expriment à travers le vecteur contrainte de Cauchy, défini par :
\[
\mathbf{T}|_{\Gamma_0} = \boldsymbol{\sigma}|_{\Gamma_0} \cdot \mathbf{n}, \quad \text{avec } \mathbf{n} = -\mathbf{e}_3.
\]
1.2 Calcul de la résultante et du moment
Nous cherchons maintenant à déterminer la résultante \(\mathbf{R}\) et le moment \(\mathbf{M}_O\) des forces gravitaires agissant sur le cylindre.
1.2.1 Résultante des forces de pesanteur
La résultante des forces \(\mathbf{R}\) représente la somme vectorielle de toutes les forces de pesanteur agissant sur le cylindre. Nous la calculons à partir de son expression intégrale volumique :
\[
\mathbf{R} = \iiint_{\Omega} \rho g \mathbf{e}_3 \, d\Omega \quad \bigl(\text{car } \mathbf{R}^* = \iiint_{\Omega} -\rho g \mathbf{e}_3 \, d\Omega\bigr)
\]
Passons en coordonnées cylindriques pour effectuer les intégrations. Le volume élémentaire s’écrit \(d\Omega = r\,dr\,d\theta\,dz\), ce qui donne :
\[
\mathbf{R} = \iiint_{\Omega} \rho g \, r \, d\theta \, dr \, dz \, \mathbf{e}_3
\]
En séparant les intégrales, nous obtenons :
\[
\mathbf{R} = \rho g \int_0^R r \, dr \int_0^{2\pi} d\theta \int_0^H dz \, \mathbf{e}_3
\]
soit, après calcul :
\[
\mathbf{R} = \pi \rho g H R^2 \, \mathbf{e}_3
\]
1.2.2 Moment au point \(O\)
Le moment \(\mathbf{M}_O\) représente l’effet de rotation des forces de pesanteur autour du point \(O\). Il s’exprime comme suit :
\[
\mathbf{M}_O = \iiint_{\Omega} (\mathbf{OM} \wedge \rho g \mathbf{e}_3) \, d\Omega \quad \bigl(\text{car } \mathbf{M}_O^* = \iiint_{\Omega} (\mathbf{OM} \wedge \rho g \mathbf{e}_3) \, d\Omega\bigr)
\]
La position \(\mathbf{OM}\) en coordonnées cylindriques est donnée par \(\mathbf{OM} = r \mathbf{e}_r + z \mathbf{e}_3\). En utilisant les propriétés des produits vectoriels \(\mathbf{e}_r \wedge \mathbf{e}_3 = -\mathbf{e}_\theta\) et \(\mathbf{e}_3 \wedge \mathbf{e}_3 = \mathbf{0}\), nous obtenons :
\[
\mathbf{M}_O = \rho g \int_0^H dz \int_0^{2\pi} d\theta \int_0^R r \, dr \, (-r \mathbf{e}_\theta)
\]
Or, \(\mathbf{e}_\theta = -\sin\theta \, \mathbf{e}_1 + \cos\theta \, \mathbf{e}_2\).
Les contributions intégrées sur \(\theta \in [0, 2\pi]\) s’annulent par symétrie du problème, ce qui conduit à :
\[
\mathbf{M}_O = \mathbf{0}
\]
1.2.3 Distribution surfacique d’efforts sur \(\Gamma_0\)
La force surfacique uniforme sur la base \(\Gamma_0\) s’écrit :
\[
\mathbf{F}_s = P \mathbf{e}_3,
\]
où \(P\) est une constante à déterminer. En intégrant cette densité surfacique sur \(\Gamma_0\) (dont l’aire est \(S = \pi R^2\)), la résultante s’obtient par :
\[
\iint_{\Gamma_0} \mathbf{F}_s \, ds = P S \mathbf{e}_3 = \mathbf{R}.
\]
En substituant l’expression de \(\mathbf{R} = \pi \rho g H R^2 \mathbf{e}_3\), il vient :
\[
P = \rho g H.
\]
Par conséquent, le torseur des efforts exercés sur la base \(\Gamma_0\) est équivalent à une distribution uniforme \(\mathbf{F}_s = P \mathbf{e}_3\) avec \(P = \rho g H\).
- Pour construire une solution analytique du problème, nous considérons à partir de maintenant le problème d’équilibre obtenu en >remplaçant la condition d’encastrement sur \(\Gamma_0\) par une condition aux limites en efforts.
La base \(\Gamma_0\) est désormais supposée soumise à une densité surfacique d’efforts uniforme :
\[
\mathbf{F}_s = P \boldsymbol{e}_3,
\]
déterminée dans la question précédente. - Écrire les équations du problème et les nouvelles conditions aux limites associées. - Vérifier si ce problème est régulier. Si oui, préciser de quel type. - Définir les espaces des champs admissibles cinématiquement, \({U}_{ad}\), et statiquement, \(\Sigma_{ad}\), pour ce problème.
3.1. Résolution du problème d’élastostatique : Calcul de \(\boldsymbol{\sigma}_{33}\)
3.1.1 Équation d’équilibre local
En adoptant l’expression simplifiée du tenseur des contraintes proposée, nous avons :
\[
\boldsymbol{\sigma} =
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & \sigma_{33}
\end{bmatrix}.
\]
La condition d’équilibre local \(\mathrm{div}\,\boldsymbol{\sigma} = \rho g \mathbf{e}_3\) s’écrit alors :
\[
\mathrm{div}\,\boldsymbol{\sigma} =
\begin{bmatrix}
0\\
0 \\
\frac{\partial \sigma_{33}}{\partial x_3}
\end{bmatrix}
= \rho g \mathbf{e}_3.
\]
Ce qui donne l’équation différentielle suivante :
\[
\frac{\partial \sigma_{33}}{\partial x_3} = \rho g.
\]
En intégrant cette équation, nous obtenons :
\[
\sigma_{33} = \rho g x_3 + f(x_1, x_2),
\]
où \(f(x_1, x_2)\) est une fonction de \(x_1\) et \(x_2\) à déterminer à partir des conditions aux limites.
3.1.2 Application des conditions aux limites
Sur la base supérieure \(\Gamma_1\) (pour \(x_3 = H\)), la surface est libre d’efforts. La condition aux limites s’écrit donc :
\[
\boldsymbol{\sigma} \cdot \mathbf{n} = \mathbf{0}, \quad \text{avec } \mathbf{n} = \mathbf{e}_3.
\] \[
\sigma_{33}(x_3 = H) = 0.
\]
En remplaçant \(x_3 = H\) dans l’expression de \(\sigma_{33}\), il vient :
\[
\rho g H + f(x_1, x_2) = 0 \quad \Longrightarrow \quad f(x_1, x_2) = -\rho g H.
\]
3.1.3 Expression finale de \(\sigma_{33}\)
En regroupant les résultats obtenus, \(\sigma_{33}\) s’écrit finalement :
\[
\sigma_{33} = \rho g (x_3 - H),
\]
où \(x_3 \in [0, H]\).
3.2 Vérification des conditions aux limites
3.2.1 Condition sur \(\Gamma_1\) (pour \(x_3 = H\))
\[
\sigma_{33}(x_3 = H) = \rho g (H - H) = 0.
\]
3.2.2 Condition sur \(\Gamma_0\) (pour \(x_3 = 0\))
\[
\sigma_{33}(x_3 = 0) = \rho g (0 - H) = -\rho g H.
\]
3.2.3 Condition sur \(\Gamma_l\) (surface latérale)
Sur \(\Gamma_l\), la normale est \(\mathbf{n} = \mathbf{e}_r = \cos\theta \, \mathbf{e}_1 + \sin\theta \, \mathbf{e}_2\).
\[
\boldsymbol{\sigma} \cdot \mathbf{e}_r = \mathbf{0}.
\]
6.4 Conclusion de l’étude du déplacement
Déplacement du centre \(O'\) de la surface \(\Gamma_1\) : En prenant \(r = 0\), nous obtenons :
\[\mathbf{OM}' = H \mathbf{e}_3 - \frac{\rho g}{2E} H^2 \mathbf{e}_3.\]
Le centre \(O'\) subit donc un déplacement vertical donné par :
\[u_z(O') = -\frac{\rho g}{2E} H^2.\]
Déplacement d’un point quelconque de \(\Gamma_1\) : La déformée de la surface \(\Gamma_1\) est décrite par :
\[u_z(r) = \frac{\nu \rho g}{E} \frac{r^2}{2} - \frac{\rho g}{2E} H^2.\]
Cette déformation se caractérise par une courbure parabolique selon la direction verticale (\(\mathbf{e}_3\)). Elle prend la forme d’un paraboloïde de révolution dont l’axe coincide avec l’axe \(\mathbf{e}_3\) du cylindre. Le sommet de ce paraboloïde est légèrement abaissé sous l’effet du poids propre, comme l’indique le terme \(-\frac{\rho g H^2}{2E}\). La courbure de la surface dépend des paramètres mécaniques du matériau, notamment du coefficient de Poisson \(\nu\), de la masse volumique \(\rho\) et du module de Young \(E\).
- Déterminer le champ de déformations associé à ce champ de contraintes.
- Existe-t-il un champ de déplacement qui en dérive ?
4. Calcul de \(\boldsymbol{\varepsilon}\) et vérification de la compatibilité
4.3 Vérification des équations de compatibilité géométrique
Le champ de déformations \(\boldsymbol{\varepsilon}\) obtenu est diagonal, avec uniquement les composantes diagonales (\(\varepsilon_{11}\), \(\varepsilon_{22}\), \(\varepsilon_{33}\)) non nulles. Vérifions que ces déformations satisfont les équations de compatibilité géométrique.
Pour la composante \(\varepsilon_{33}\) :
L’équation de compatibilité correspondante s’écrit :
$ {33,11} + {11,33} = 2, _{13,13} $.
Puisque \(\varepsilon_{13} = 0\), le terme de droite est nul. Par ailleurs, \(\varepsilon_{33}\) ne dépend que de \(x_3\), donc \(\varepsilon_{33,11} = 0\). Enfin, \(\varepsilon_{11}\) dépend linéairement de \(x_3\), d’où \(\varepsilon_{11,33} = 0\). L’équation est bien satisfaite.
Pour les composantes \(\varepsilon_{11}\) et \(\varepsilon_{22}\) :
Ces composantes dépendent linéairement de \(x_3\), donc leurs dérivées secondes par rapport à \(x_3\) sont nulles :
$ {11,33} = 0 $ et $ {22,33} = 0 $.
Les équations de compatibilité correspondantes sont donc satisfaites.
Pour les autres composantes :
Puisque \(\boldsymbol{\varepsilon}\) ne dépend que de la variable \(x_3\), toutes les dérivées secondes mixtes ou d’ordre supérieur en \(x_1\) et \(x_2\) sont nulles. Ces composantes ne présentent aucune incompatibilité.
4.4 Conclusion
L’ensemble des équations de compatibilité géométrique est satisfait par le champ de déformations \(\boldsymbol{\varepsilon}\) proposé. Ce résultat démontre que ce champ de déformations est géométriquement cohérent, c’est-à-dire qu’il peut être associée à un champ de déplacement \(\mathbf{u}\) continu et régulier dans tout le domaine \(\Omega\).
En d’autres termes, la solution obtained pour \(\boldsymbol{\varepsilon}\) respecte les lois de la géométrie de la mécanique des milieux continus. Il n’y a aucune incohérence ni distorsion impossible dans le matériau, et le champ \(\mathbf{u}\) est physiquement réalisable.
- Calculer le champ de déplacement associé s’il existe.
- Le problème résolu admet-il un couple \((\sigma, u)\) solution unique ? Commenter par rapport au problème initial.
5. Calcul du champ de déplacement par intégration des déformations
Le tenseur des déformations \(\boldsymbol{\varepsilon}\) est diagonal. Il s’écrit :
\[
\boldsymbol{\varepsilon} =
\begin{bmatrix}
\varepsilon_{11} & 0 & 0 \\
0 & \varepsilon_{22} & 0 \\
0 & 0 & \varepsilon_{33}
\end{bmatrix},
\]
avec :
- \(\varepsilon_{11} = \varepsilon_{22} = -\frac{\nu}{E} \rho g (x_3 - H)\),
- \(\varepsilon_{33} = \frac{1}{E} \rho g (x_3 - H)\).
5.2 Intégration des équations de Green-Lagrange
Procédons à l’intégration de chaque équation :
a) Pour \(\varepsilon_{11}\) :
\[
\varepsilon_{11} = \frac{\partial u_1}{\partial x_1} = -\frac{\nu}{E} \rho g (x_3 - H).
\] En intégrant par rapport à \(x_1\), nous obtenons :
\[
u_1 = -\frac{\nu}{E} \rho g (x_3 - H) x_1 + f_1(x_2, x_3).
\]
b) Pour \(\varepsilon_{22}\) :
\[
\varepsilon_{22} = \frac{\partial u_2}{\partial x_2} = -\frac{\nu}{E} \rho g (x_3 - H).
\] En intégrant par rapport à \(x_2\), nous obtenons :
\[
u_2 = -\frac{\nu}{E} \rho g (x_3 - H) x_2 + f_2(x_1, x_3).
\]
c) Pour \(\varepsilon_{33}\) :
\[
\varepsilon_{33} = \frac{\partial u_3}{\partial x_3} = \frac{1}{E} \rho g (x_3 - H).
\] En intégrant par rapport à \(x_3\), nous obtenons :
\[
u_3 = \frac{1}{E} \rho g \frac{(x_3 - H)^2}{2} + f_3(x_1, x_2).
\]
5.4 Exploitation des conditions de compatibilité
Injectons les expressions de \(u_1\), \(u_2\) et \(u_3\) dans les équations de compatibilité (4), (5) et (6). Nous obtenons les conditions suivantes sur les fonctions \(f_1\), \(f_2\) et \(f_3\) :
Condition (4) (pour \(\varepsilon_{12} = 0\)) :
\[
\frac{\partial f_1}{\partial x_2}(x_2, x_3) + \frac{\partial f_2}{\partial x_1}(x_1, x_3) = 0.
\]
Condition (5) (pour \(\varepsilon_{13} = 0\)) :
\[
\frac{\partial f_1}{\partial x_3}(x_2, x_3) - \frac{\nu \rho g}{E} x_1 + \frac{\partial f_3}{\partial x_1}(x_1, x_2) = 0.
\]
Condition (6) (pour \(\varepsilon_{23} = 0\)) :
\[
\frac{\partial f_2}{\partial x_3}(x_1, x_3) - \frac{\nu \rho g}{E} x_2 + \frac{\partial f_3}{\partial x_2}(x_1, x_2) = 0.
\]
5.2 Calcul du champ de déplacement
- Le champ de déplacement \(\mathbf{u}\) a été calculé et décomposé en trois parties :
- Déformation mécanique,
- Rotation de corps rigide, et
- Translation de corps rigide.
\[
\mathbf{u} =
\begin{cases}
u_1 = -\frac{\nu \rho g}{E} (x_3 - H) x_1 + a x_2 + b x_3 + d, \\
u_2 = -\frac{\nu \rho g}{E} (x_3 - H) x_2 - a x_1 + f x_3 + h, \\
u_3 = \frac{\rho g}{E} \left( \frac{x_3^2}{2} - H x_3 \right) + \frac{\nu \rho g}{E} \frac{x_1^2 + x_2^2}{2} + b x_1 - f x_2 + n.
\end{cases}
\]
- Ce champ satisfait à la fois les équations de compatibilité et les conditions aux limites imposées, prouvant qu’il est admissible et géométriquement cohérent.
5.9 Unicité de la solution
L’analyse du problème révèle que le couple solution \((\boldsymbol{\sigma}, \mathbf{u})\) n’est pas unique. Examinons les raisons de cette non-unicité.
Dans le problème initial (avec encastrement sur \(\Gamma_0\)) : - La condition d’encastrement sur \(\Gamma_0\) imposait l’annulation du déplacement :
$$
\mathbf{u} = \mathbf{0} \quad \text{sur } \Gamma_0,
$$
ce qui éliminait toute contribution de rotation ou de translation de corps rigide.
- Par conséquent, pour le problème initial avec encastrement, la solution \((\boldsymbol{\sigma}, \mathbf{u})\) est unique.
Dans le problème modifié (avec chargement en efforts sur \(\Gamma_0\)) : - Le remplacement de la condition d’encastrement par un chargement en efforts uniformes assouplit considérablement les contraintes sur les déplacements. - Cette modification introduit des degrés de liberté supplémentaires correspondant aux mouvements de corps rigide (rotation et translation). - Ces mouvements rigides ne sont pas contraints par les équations d’équilibre ni par les conditions aux limites en efforts. - En conséquence, la solution \((\boldsymbol{\sigma}, \mathbf{u})\) est non unique.
Cette non-unicité se manifeste par la présence des six constantes indéterminées \(a\), \(b\), \(f\), \(d\), \(h\) et \(l\), qui représentent les mouvements rigides possibles du système.
5.5 Résolution des équations de compatibilité
En derivant les conditions précédentes, nous obtenons les équations différentielles suivantes :
Dérivée de la condition (4) :
\[
\frac{\partial^2 f_1}{\partial x_2^2}(x_2, x_3) = 0 \quad \text{et} \quad \frac{\partial^2 f_2}{\partial x_1^2}(x_1, x_3) = 0.
\]
Dérivée de la condition (5) :
\[
\frac{\partial^2 f_1}{\partial x_3^2}(x_2, x_3) = 0 \quad \text{et} \quad -\frac{\nu \rho g}{E} + \frac{\partial^2 f_3}{\partial x_1^2}(x_1, x_2) = 0.
\]
Dérivée de la condition (6) :
\[
-\frac{\nu \rho g}{E} + \frac{\partial^2 f_3}{\partial x_2^2}(x_1, x_2) = 0 \quad \text{et} \quad \frac{\partial^2 f_2}{\partial x_3^2}(x_1, x_3) = 0.
\]
5.7 Détermination des constantes d’intégration
En reportant les expressions de \(f_1\), \(f_2\) et \(f_3\) dans les conditions de compatibilité (4), (5) et (6), nous déterminons les relations entre les constantes d’intégration :
Dans la condition (4) :
\[
a + e + (c + g)x_3 = 0,
\] ce qui impose :
\[
a + e = 0 \quad \text{et} \quad c + g = 0.
\]
Dans la condition (5) :
\[
b + i = 0 \quad \text{et} \quad c + k = 0.
\]
Dans la condition (6) :
\[
f + j = 0 \quad \text{et} \quad g + k = 0.
\]
Ces relations permettent d’exprimer toutes les constantes en fonction de six paramètres indépendants.
5.8 Expression finale du champ de déplacement
En assemblesant l’ensemble des résultats, le champ de déplacement \(\mathbf{u}\) s’écrit :
\[
\mathbf{u} =
\begin{cases}
u_1 = -\dfrac{\nu \rho g}{E} (x_3 - H) x_1 + a x_2 + b x_3 + d, \\
u_2 = -\dfrac{\nu \rho g}{E} (x_3 - H) x_2 - a x_1 + f x_3 + h, \\
u_3 = \dfrac{\rho g}{E} \left( \dfrac{x_3^2}{2} - H x_3 \right) + \dfrac{\nu \rho g}{E} \dfrac{x_1^2 + x_2^2}{2} + b x_1 - f x_2 + l.
\end{cases}
\]
Ce champ peut être décomposé en trois contributions distinctes : - une partie liée à la déformation mécanique (effet des contraintes internes), - une partie associée à une rotation de corps rigide (paramètres \(a\) et \(b\)), - une partie correspondant à une translation de corps rigide (paramètres \(d\), \(h\) et \(l\)).
Ce champ satisfait simultanément les équations de compatibilité géométrique et les conditions aux limites en efforts, ce qui démontre son caractère admissible.
- Déterminer le déplacement du point \(O'\), centre de la face \(\Gamma_1\), ainsi que la déformée de cette surface.
6. Déplacement de la face supérieure \(\Gamma_1\)
Considérons un point \(M_0\) appartenant à la surface \(\Gamma_1\), caractérisé par les coordonnées \((r, \theta, x_3 = H)\) en coordonnées cylindriques. Sa position initiale est donnée par :
\[
\mathbf{OM}_0 = r \mathbf{e}_r + H \mathbf{e}_3.
\]
Après déformation, sa position devient :
\[
\mathbf{OM} = \mathbf{OM}_0 + \mathbf{u}(M_0),
\]
où \(\mathbf{u}(M_0)\) désigne le déplacement du point \(M_0\) évaluée sur \(\Gamma_1\) (c’est-à-dire pour \(x_3 = H\)).
6.1 Calcul du déplacement sur \(\Gamma_1\)
À partir du champ de déplacement \(\mathbf{u}\) déterminé précédemment, évaluons chaque composante sur la surface \(\Gamma_1\) (pour \(x_3 = H\)) :
Composante radiale \(u_r\) : En coordonnées cylindriques, la composante radiale s’annule pour \(x_3 = H\), car seul le terme de déformation mécanique contribue :
\[
u_r = 0.
\]
Composante orthoradiale \(u_\theta\) : En raison de la symétrie axisymétrique du problème, il n’y a pas de dépendance angulaire. Par conséquent :
\[u_\theta = 0.\]
Composante verticale \(u_z\) : La composante verticale est obtenue en évaluant \(u_3\) en \(x_3 = H\) :
\[u_z = \frac{\nu \rho g}{E} \frac{r^2}{2} - \frac{\rho g}{2E} H^2.\]
6.4 Conclusion
Déplacement du centre \(O'\) de \(\Gamma_1\) : En posant \(r = 0\), on retrouve :
\[\mathbf{OM}' = H \mathbf{e}_3 - \frac{\rho g}{2E} H^2 \mathbf{e}_3.\]
Le point \(O'\) subit donc un déplacement vertical de :
\[u_z(O') = -\frac{\rho g}{2E} H^2.\]
Déplacement général sur \(\Gamma_1\) : La déformée de la surface \(\Gamma_1\) est donnée par :
\[u_z(r) = \frac{\nu \rho g}{E} \frac{r^2}{2} - \frac{\rho g}{2E} H^2.\]
La déformation est caractérisée par une courbure parabolique dans la direction verticale (\(\mathbf{e}_3\)). Elle prend la forme d’un paraboloïde de révolution orienté selon l’axe \(\mathbf{e}_3\). Le sommet de ce paraboloïde est légèrement abaissé en raison du poids propre, ce qui est exprimé par le terme \(-\frac{\rho g H^2}{2E}\). La courbure de la surface dépend des paramètres mécaniques du matériau, notamment le coefficient de Poisson (\(\nu\)), la masse volumique (\(\rho\)) et le module de Young (\(E\)).
- Calculer numériquement le déplacement \(u_z(O')\), au centre de \(\Gamma_1\), pour ces dimensions et propriétés mécaniques. Comparer ce résultat à celui obtenu à l’aide d’une simulation par éléments finis 3D. Interpréter les écarts éventuels.
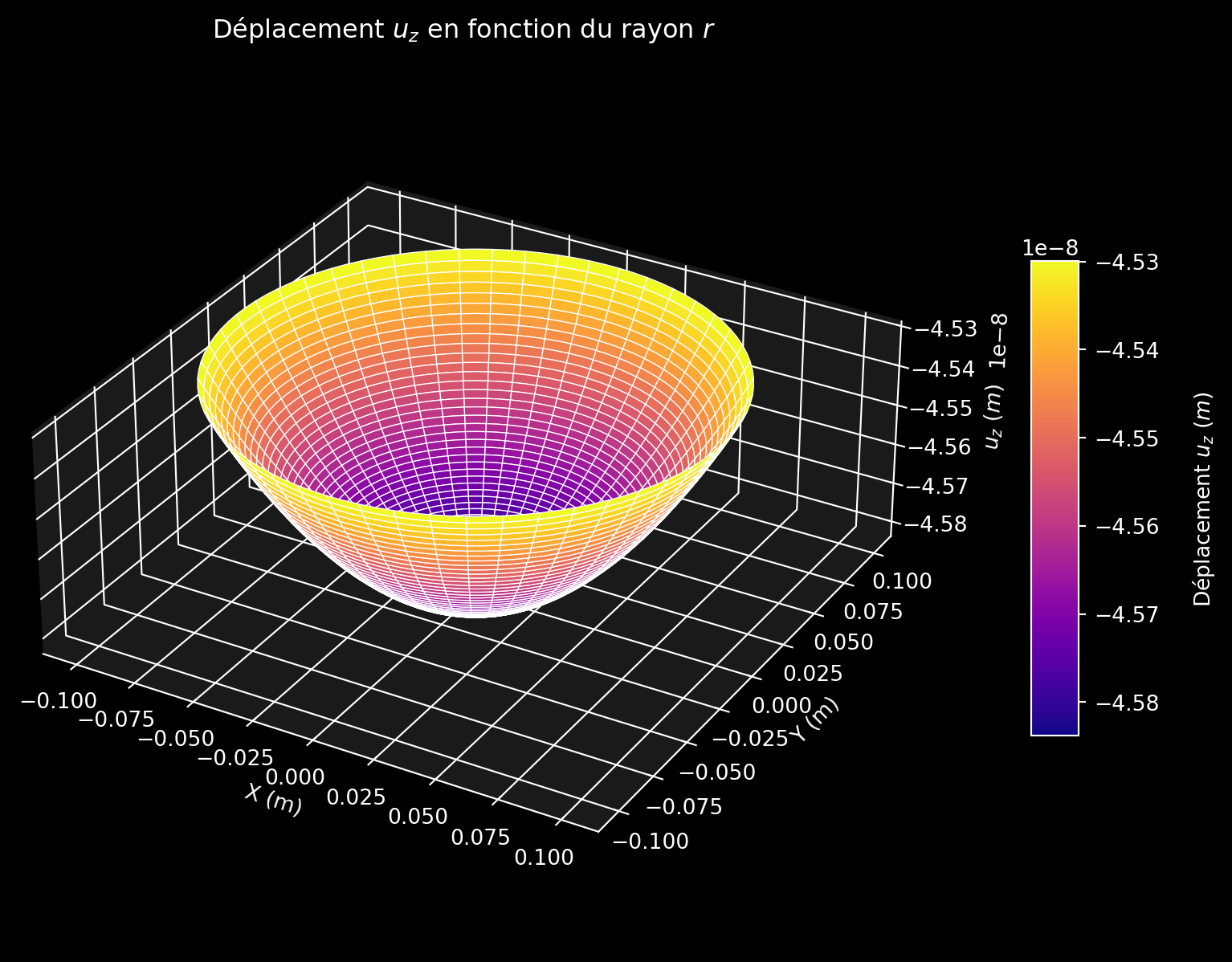
 Figure 1.1 : Représentation du cylindre avec ses surfaces principales.
Figure 1.1 : Représentation du cylindre avec ses surfaces principales.